Robot Coin Collection Problem : Several coins are placed in cells of an n × m board, no more than one coin per cell.A robot, located in the upper left cell of the board, needs to collect as many of the coins as possible and bring them to the bottom right cell. On each step, the robot can move either one cell to the right or one cell down from its current location. When the robot visits a cell with a coin, it always picks up that coin. Design an algorithm to find the maximum number of coins the robot can collect and a path it needs to follow to do this.
We will take double dimensional array F(i,j) here, fill it along the path where robot can collect maximum number of coins. The last cell of F(i,j) will have the maximum number of coins. As the problem states that the Robot can move only to the bottom or right therefore if Robot is at cell (i,j) means Robot is here either from above row (i-1, j) or from previous column (i , j-1). The largest numbers of coins that can be brought to these cells are maximum of F(i − 1, j) and F(i, j − 1) plus one possible coin at cell (i, j ) itself. We can derive following formula for this recurrence.
F[i, j] = max{F[i − 1, j ], F[i, j − 1]} + coins[i,j] for 1≤ i ≤ n, 1≤ j ≤ m
F[0, j] = 0 for 1≤ j ≤ m and F[i, 0] = 0 for 1≤ i ≤ n
Algorithm
public class RobotCoinCollection {
public static int collectCoins(int[][] coinBoard) {
int rowLen = coinBoard.length;
int columnLen = coinBoard[0].length;
int[][] F = new int[rowLen][columnLen];
F[0][0] = coinBoard[0][0];
for (int column = 1; column < columnLen; column++) {
F[0][column] = F[0][column - 1] + coinBoard[0][column];
}
for (int row = 1; row < rowLen; row++) {
F[row][0] = F[row - 1][0] + coinBoard[row][0];
for (int column = 1; column < columnLen; column++) {
F[row][column] = max(F[row - 1][column], F[row][column - 1]) + coinBoard[row][column];
}
}
// Just to understand
System.out.println("F[][]");
System.out.println("-------------");
for (int row = 0; row < 5; row++) {
for (int column = 0; column < 5; column++) {
System.out.print(F[row][column] + " ");
}
System.out.println();
}
return F[rowLen - 1][columnLen - 1];
}
private static int max(int i, int j) {
return i > j ? i : j;
}
public static void main(String[] args) {
int[][] coinBoard = new int[5][5];
coinBoard[0][0] = 1;
coinBoard[1][1] = 1;
coinBoard[1][3] = 1;
coinBoard[2][2] = 1;
coinBoard[4][2] = 1;
coinBoard[4][4] = 1;
System.out.println("coinBoard[][]");
System.out.println("-------------");
for (int row = 0; row < 5; row++) {
for (int column = 0; column < 5; column++) {
System.out.print(coinBoard[row][column] + " ");
}
System.out.println();
}
System.out.println("Maximum Coins : "+collectCoins(coinBoard));
}
}
Levenshtein Word Distance : The Levenshtein distance algorithm is used to find difference between two words using the smallest number of insertions, deletions, and substitutions required to transform one word into another.
For ex: consider words : abcdej and abfdh
The Levenshtein distance will be 3 – there are 2 substitution c to f, e to h and 1 deletion of h.
We are always free to choose threshold limit to under which we can accept a word. Levenshtein distance technique used in number of applications including word processor spell-checking, DNA matching, and plagiarism detection.
Three different operations can be performed. Each operation is assigned a cost, and the smallest distance is the set of changes with the smallest total cost. To calculate the Levenshtein distance, start by creating a grid with rows and columns corresponding to the letters in the source and target word.
Following is the recurrence relation for Levenshtein Distance:
F(i,j) = min{F(i-1, j) +1, F(i, j-1) +1, F(i-1, j-1) + s[i]!=t[i]? 1:0},
F(0,0) = 0
If you are finding it difficult to understand recurrence then don’t worry, read below example carefully.
Below figure shows the grid for calculating the edit distance from “dynamic” to “dnamsic”.
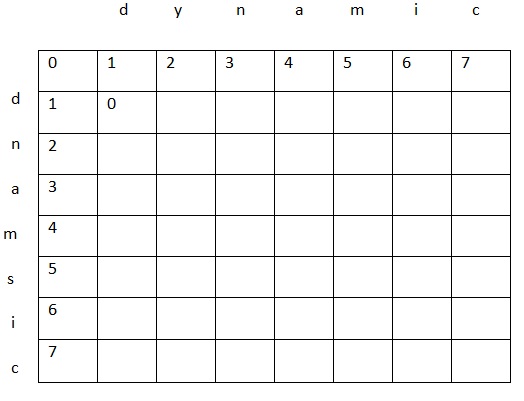
There is an extra row and column inserted. The row corresponds to an empty source word and the values represent the cumulative cost of inserting each character. The column corresponds to an empty target word and the values represent the cumulative cost of deletion.
The next step is to calculate the values for each of the remaining cells in the grid. The above recurrence can be written as below. You can easily understand it.
min(left diagonal + substitution cost, above + delete cost, left + insert cos)
Substitution cost = 1 if source[i] ! = target[i] otherwise 0,
deletion cost = 1 (always),
insertion cost = 1 (always)
For example, to calculate the value for the first cell (d, d), you apply the following formula:
min(0 + 0, 1 + 1, 1 + 1) = min(0, 2, 2) = 0
The cost for insertion and deletion is always one, but the cost for substitution is only one when the source and target characters don’t match.
Algorithm
public class LevenshteinWordDistance {
private static final int SUBSTITUTION_COST = 1;
private static final int DELETION_COST = 1;
private static final int INSERTION_COST = 1;
public static int calculateLavenshteinDistance(String source, String target) {
assert source != null : "source can't be null";
assert target != null : "target can't be null";
int sourceLength = source.length();
int targetLength = target.length();
int[][] F = new int[sourceLength + 1][targetLength + 1];
F[0][0] = 0;
for (int row = 1; row <= sourceLength; ++row) {
F[row][0] = row;
}
for (int col = 1; col <= targetLength; ++col) {
F[0][col] = col;
}
for (int row = 1; row <= sourceLength; ++row) {
for (int col = 1; col <= targetLength; ++col) {
F[row][col] = min(substitutionCost(source, target, F, row, col),
deleteCost(F, row, col),
insertCost(F, row, col));
}
}
return F[sourceLength][targetLength];
}
private static int substitutionCost(String source, String target, int[][] F, int row, int col) {
int cost = 0;
if (source.charAt(row - 1) != target.charAt(col - 1)) {
cost = SUBSTITUTION_COST;
}
return F[row - 1][col - 1] + cost;
}
private static int deleteCost(int[][] F, int row, int col) {
return F[row - 1][col] + DELETION_COST;
}
private static int insertCost(int[][] F, int row, int col) {
return F[row][col-1] + INSERTION_COST;
}
private static int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
public static void main(String[] args) {
String source = "dynamic";
String target = "dnamsic";
System.out.println("LevenshteinWordDistance:: "+calculateLavenshteinDistance(source, target));
}
}
Output
--------
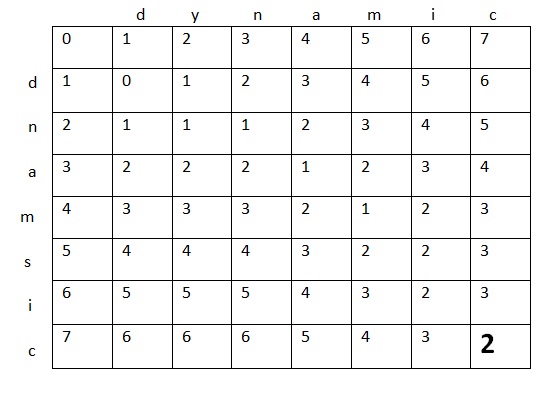
LevenshteinWordDistance:: 2
Try to fill the above grid using the above formula, you will get following filled grid.
The last cell will have the final result.
References
Algorithm Design Manual – Steven S. Skiena
Design and Analysis of Algorithm – Anany Levitin
Beginning Algorithm – Simon Harris, James Ross
Data Structure And Algorithm with javaScript – Michael McMillan


hey thanks for the knowledge, but I think you might put the same table picture two times in coin row problem explaination.