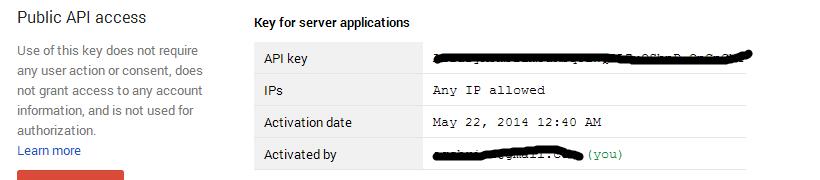
TDD (Test Driven Development) By Example
What is Test driven development?
Write code only to fix a failing test case. That is the gist of test driven development (TDD). This is a cyclic process- You first write a test for a requirement, and then you write some real code to pass the test, then you refactor the code for best possible design using various design principle for example SOLID , GRASP etc. The benefit here is that you already have a safety net as tests before refactoring the code. Whatever refactoring you are doing, your tests should not fail.
TDD is an evolving process. You evolve your software design by simply following above steps for each and every requirements of your software. It keeps you away from verbose code, over engineering and making unnecessary assumption.
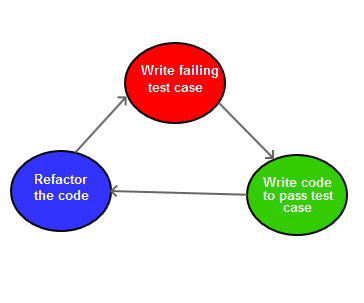
The Test->Code->Refactor cycle also known as red-green-blue. You can understand the significance of these colours from below diagram.
Since the title of this post is TDD by example, let’s do an example using TDD to understand the concepts better.
We will follow the same cycle
Write a failing test – make it pass – refactor the code.
The problem is:
Create a simple shopping cart
We will add different requirements to our current problem and we evolve our design and code accordingly.
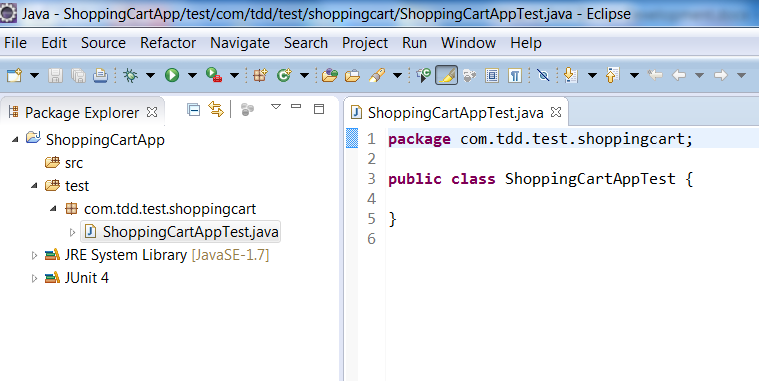
Create a simple java project ShoppingCartApp in Eclipse, add JUnit4 library dependency to it. First create a test folder and a class ShoppingCartAppTest.
Requirement: Create an empty shopping cart
When: An empty shopping cart created.
Then: the product count of cart should be 0.
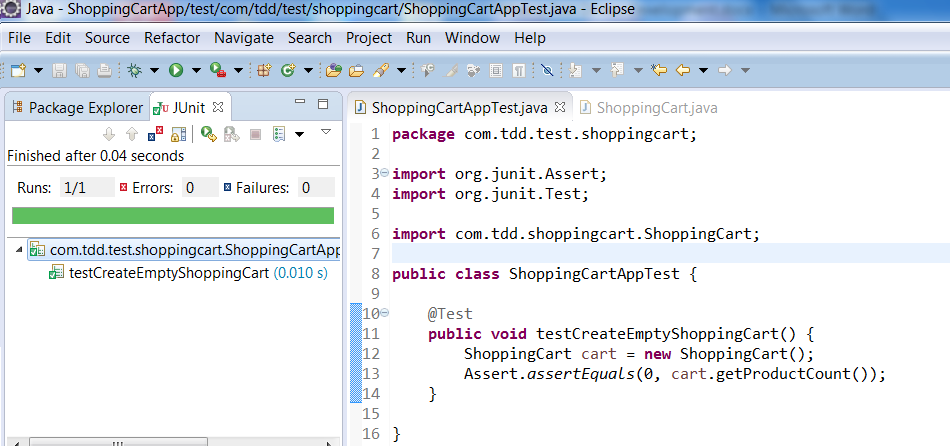
Add a test to create an empty shopping cart in ShoppingCartAppTest class. Make an assertion to product count 0.
package com.tdd.test.shoppingcart;
import org.junit.Assert;
import org.junit.Test;
public class ShoppingCartAppTest {
@Test
public void testCreateEmptyShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Assert.assertEquals(0, cart.getProductCount());
}
}
Now it is giving compilation error since we don’t have ShoppingCart class. Let’s create a ShoppingCart class in src folder and a method getProductCount() in it.
package com.tdd.shoppingcart;
public class ShoppingCart {
public int getProductCount() {
return 0;
}
}
Now run the test case. It should pass. We have completed our first requirement using TDD.
Requirement: Add Product to shopping cart
When: Add 1 unit of ‘Gatsby hair cream’, unit price 30 Rupees.
Then:
– The product count of the cart should be 1.
– The total value of cart should be 30 rupees.
Add a test to add a Product to ShoppingCart. Make assertion for product count 1 and then later make the assertion for the total cart value should be 30.
import org.junit.Assert;
import org.junit.Test;
import com.tdd.shoppingcart.Product;
import com.tdd.shoppingcart.ShoppingCart;
public class ShoppingCartAppTest {
@Test
public void testCreateEmptyShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Assert.assertEquals(0, cart.getProductCount());
}
@Test
public void testAddSingleProductToShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Product product = new Product("Gatsby hair cream", 1, 30.0);
cart.addProduct(product);
Assert.assertEquals(1, cart.getProductCount());
}
}
It will give you compilation error since we don’t have Product class and also there is no addProduct() method to our ShoppingCart class.
Let’s create the Product class as per our requirement.
package com.tdd.shoppingcart;
public class Product {
private String productName;
private int quantity;
private double totalPrice;
public Product(String productName, int quantity, double totalPrice) {
this.productName = productName;
this.quantity = quantity;
this.totalPrice = totalPrice;
}
public String getProductName() {
return productName;
}
public void setProductName(String productName) {
this.productName = productName;
}
public int getQuantity() {
return quantity;
}
public void setQuantity(int quantity) {
this.quantity = quantity;
}
public double getTotalPrice() {
return totalPrice;
}
public void setTotalPrice(double totalPrice) {
this.totalPrice = totalPrice;
}
}
Add ‘addProduct()’ method to ShoppingCart class.
package com.tdd.shoppingcart;
public class ShoppingCart {
public int getProductCount() {
return 0;
}
public void addProduct(Product product) {
}
}
Now you have failing test since in reality there is no product added to ShoppingCart.
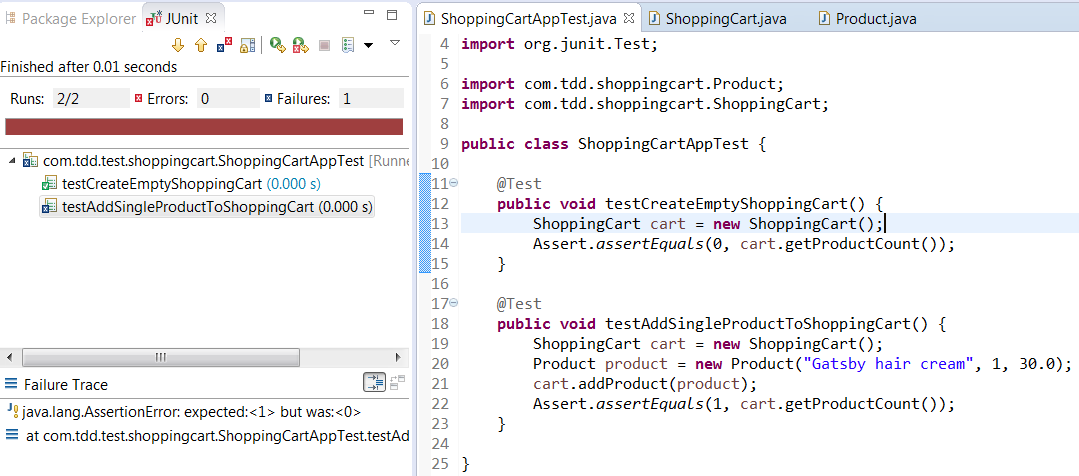
It’s time to refactor our ShoppingCart class. Let’s add a product holder to ShoppingCart class and add products to it.
package com.tdd.shoppingcart;
import java.util.ArrayList;
import java.util.List;
public class ShoppingCart {
private List<Product> productList = new ArrayList<>();
public int getProductCount() {
return productList.size();
}
public void addProduct(Product product) {
productList.add(product);
}
}
Run your test again. You can see your test is passing now.
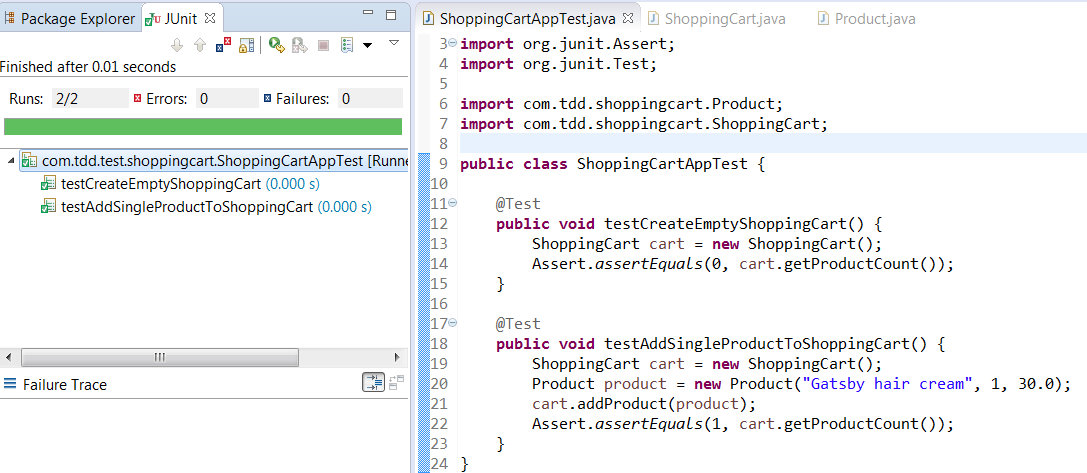
We have completed the first part of the requirement. Now add an assertion for the second requirement- the total cart value should be 30.0.
package com.tdd.test.shoppingcart;
import org.junit.Assert;
import org.junit.Test;
import com.tdd.shoppingcart.Product;
import com.tdd.shoppingcart.ShoppingCart;
public class ShoppingCartAppTest {
@Test
public void testCreateEmptyShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Assert.assertEquals(0, cart.getProductCount());
}
@Test
public void testAddSingleProductToShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Product product = new Product("Gatsby hair cream", 1, 30.0);
cart.addProduct(product);
Assert.assertEquals(1, cart.getProductCount());
Assert.assertEquals(30.0, cart.getTotalCartValue());
}
}
This will give you compilation error since we don’t have the getTotalCartValue() method in ShoppingCart class. Add this method to ShoppingCart.
package com.tdd.shoppingcart;
import java.util.ArrayList;
import java.util.List;
public class ShoppingCart {
private List<Product> productList = new ArrayList<>();
public int getProductCount() {
return productList.size();
}
public void addProduct(Product product) {
productList.add(product);
}
public double getTotalCartValue() {
return 0.0;
}
}
Now run the test. You will have failing test case.
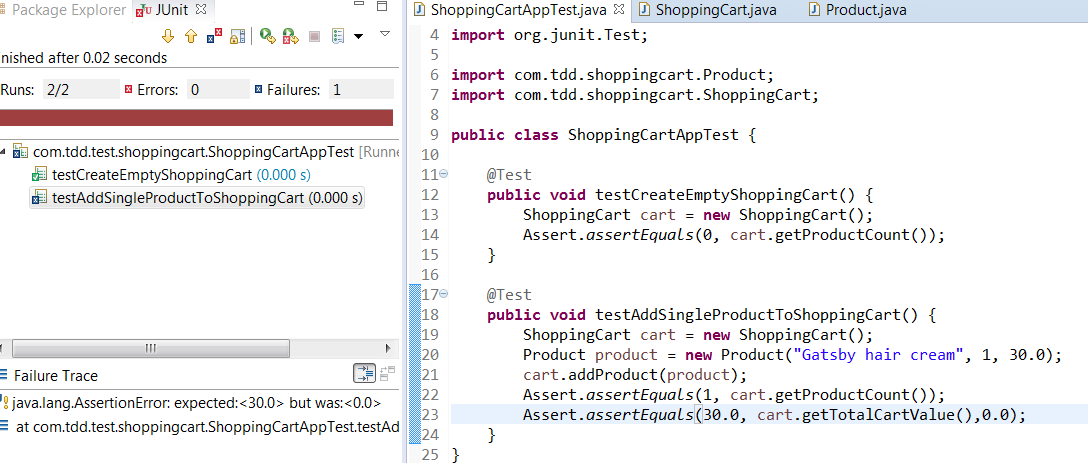
Its time to refactor our ShoppingCart class. Add some real logic to calculate cart value.
package com.tdd.shoppingcart;
import java.util.ArrayList;
import java.util.List;
public class ShoppingCart {
private List<Product> productList = new ArrayList<>();
private double totalCartValue;
public int getProductCount() {
return productList.size();
}
public void addProduct(Product product) {
productList.add(product);
}
public double getTotalCartValue() {
if (productList.size() > 0) {
for (Product product : productList) {
totalCartValue = totalCartValue + product.getTotalPrice();
}
}
return totalCartValue;
}
}
Now run the test again. You test is passing now.
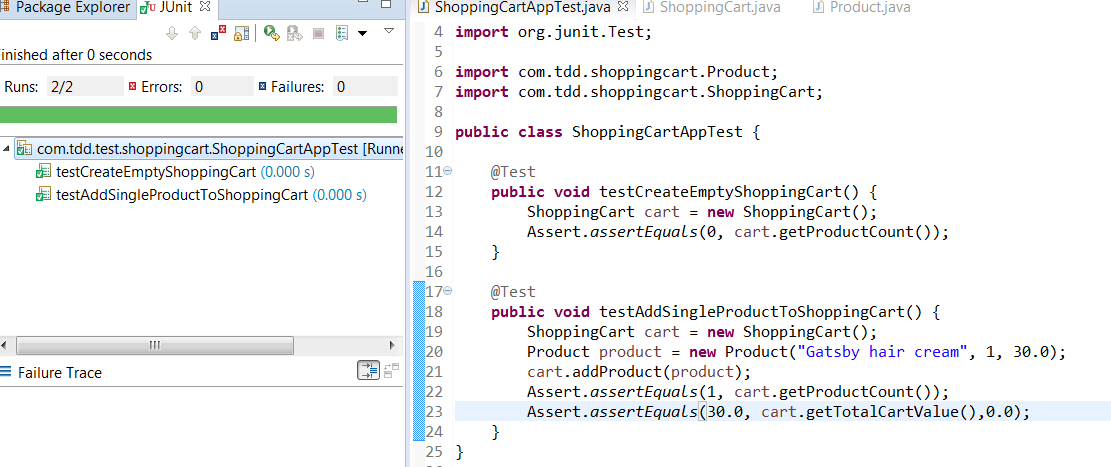
We have completed the two requirements.
Requirement: Add different Products to shopping cart
When:
– Add 1 unit of ‘Gatsby hair cream’, unit price 30 Rupees.
– Add 1 unit of ‘Bvlgiri Soap’, unit price 100 Rupees.
Then:
– The product count of the cart should be 2.
– The total value of cart should be 130 rupees.
Add a test to add different Products to ShoppingCart. Make assertion for product count 2 and the total cart value 130.
package com.tdd.test.shoppingcart;
import org.junit.Assert;
import org.junit.Test;
import com.tdd.shoppingcart.Product;
import com.tdd.shoppingcart.ShoppingCart;
public class ShoppingCartAppTest {
@Test
public void testCreateEmptyShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Assert.assertEquals(0, cart.getProductCount());
}
@Test
public void testAddSingleProductToShoppingCart() {
ShoppingCart cart = new ShoppingCart();
Product product = new Product("Gatsby hair cream", 1, 30.0);
cart.addProduct(product);
Assert.assertEquals(1, cart.getProductCount());
Assert.assertEquals(30.0, cart.getTotalCartValue(),0.0);
}
@Test
public void addDifferentProductsToTheCart(){
ShoppingCart cart = new ShoppingCart();
Product gatsByCream = new Product("Gatsby hair cream", 1, 30.0);
Product bvlgiriSoap = new Product("Bvlgiri Soap", 1, 100.0);
cart.addProduct(gatsByCream);
cart.addProduct(bvlgiriSoap);
Assert.assertEquals(2, cart.getProductCount());
Assert.assertEquals(130.0, cart.getTotalCartValue(),0.0);
}
}
Run the test, it will pass without any refactoring.
It’s time to add more requirements to our Shopping Cart application Let’s move to the next requirement (on second page).
Go to the next page – Click on the below red circle with page number.