I would highly recommend to read below posts before getting into questions on heap-
Questions On Heap
Let’s discuss some of the questions on heap which can be easily solved with the help of Heap.
Problem 1: Find the largest k numbers (in value) out of n numbers. For example, if given an array with ten numbers {1, 8, 9, 2, 10, 14, 3, 4, 7, 16 }, please return the largest five numbers 8, 10, 9, 14, 16.
This Question can also be asked as-
Describe an algorithm to find the largest 1 million numbers in 1 billion numbers. Assume that the computer memory can hold all one billion numbers.
If large numbers involved in problem – first try to solve the problem for smaller numbers.
The simple solution is to sort the n input numbers in descending order and get the first K numbers. Sorting will cost you O(nlogn) time. You can apply insertion sort for smaller number of elements.
We can achieve this in O(nlogk) time using minHeap (Parent is smaller than its children).
- Create a Min Heap with the first K numbers.
- For each remaining number, insert it in the Min Heap and then delete the minimum value from the heap.
- The heap now contains the largest K numbers.
- This algorithm is O(n log K), where K is the number of values we are looking for.
The Solution using MinHeap will work as follows.
- If the K is greater than the number of input elements- no need to do anything just return the elements
- Fill the Min Heap with K elements of input Array. For example if K=5 then the Min Heap will contain [1, 2, 9, 8, 10]. Now compare the Array[K+1] say N with top element of Min Heap, if N is greater than Heap top element- remove top element and insert N. Repeat the process up to Array.length. Finally you will have the Min Heap with K largest elements.
Let’s create a Min Heap:
public class MinHeap {
private int[] heapArray;
private int maxSize;
private int heapSize;
public MinHeap(int size) {
heapSize = 0;
maxSize = size;
heapArray = new int[maxSize];
}
public int size() {
return heapSize;
}
public int peek() {
assert heapSize <= 0 : "heap underflow";
return heapArray[0];
}
public int get(int i) {
assert heapSize <= 0 : "heap underflow";
return heapArray[i];
}
public void insertKey(int key) {
assert heapSize > maxSize - 1 : "heap overflow";
heapArray[heapSize] = key;
trickleUp(heapSize++);
}
// child dominate- parent will be smaller than children, if not then swap
private void trickleUp(int i) {
int parent = (i - 1) / 2;
while (i > 0 && heapArray[i] < heapArray[parent]) {
int temp = heapArray[parent];
heapArray[parent] = heapArray[i];
heapArray[i] = temp;
i = parent;
parent = (i - 1) / 2;
}
}
// Top will be always the minimum
public int extractMin() {
assert heapSize < 0 : "heap underflow";
int min = heapArray[0];
heapArray[0] = heapArray[--heapSize];
minHeapify(0);
return min;
}
// Parent is less than its children
public void minHeapify(int i) {
int smallest = i;
while (smallest < heapSize / 2) {
int left = (2 * i) + 1;
int right = left + 1;
if (left < heapSize && heapArray[left] < heapArray[i]) {
smallest = left;
}
if (right < heapSize && heapArray[right] < heapArray[smallest]) {
smallest = right;
}
if (smallest != i) {
int temp = heapArray[i];
heapArray[i] = heapArray[smallest];
heapArray[smallest] = temp;
i = smallest;
} else {
break;
}
}
}
}
Create a class LargestNumbersFinder:
package com.test.heap;
class LargestNumbersFinder {
public static int[] getLargestNumbers(int[] input, int k) {
// if required number of largest items is less than the given
// array, return array itself
if (input.length <= k) {
return input;
}
int[] output = new int[k];
MinHeap minHeap = new MinHeap(input.length);
// insert the array's K element to the minHeap
for (int i = 0; i < input.length; i++) {
if (minHeap.size() < k) {
minHeap.insertKey(input[i]);
} else {
if (minHeap.peek() < input[i]) {
minHeap.extractMin();
minHeap.insertKey(input[i]);
}
}
}
// Heap contains top K maximum numbers
for (int i = 0; i < minHeap.size(); i++) {
output[i] = minHeap.get(i);
}
return output;
}
public static void main(String[] args) {
int[] array = { 1, 8, 9, 2, 10, 14, 3, 4, 7, 16 };
int[] output = LargestNumbersFinder.getLargestNumbers(array, 5);
for (int key : output) {
System.out.print(key + " ");
}
}
}
Output
---------
8 10 9 14 16
If you are asked to find least k numbers then use Max Heap in similar fashion. Just change the condition if (maxHeap.getMax() > input[i])
Problem 2: You are given a set of integers in an unordered binary tree. Use an array sorting routine to transform the tree into a heap that uses a balanced binary tree as its underlying data structure.
This problem is very simple. You have an unordered binary tree means there is no specific relationship between parent and child like in Binary search tree.
One important property of sorted array is the it satisfy heap condition without calling heapify. If array is sorted in ascending order, it satisfy the Min Heap property and if sorted in Descending order, it satisfy the Max Heap property. You can give try- write some numbers on notepad in sorted order and see if it also satisfy heap condition or not.
Now in this problem, our job is to traverse the Binary tree and store it in an Array- then sort the array in ascending order – now we know that sorted array elements can be directly inserted to min heap. We have already seen that in Array if the parent index is i then left child will be at position 2*i+1 and right child will be at position 2*i+2. Using this relationship insert the array elements back to the Binary tree.
import java.util.Arrays;
import java.util.Comparator;
public class BinaryTreeToHeap {
// PreOrder traversal
public static int traverse(Node node, int count, Node[] nodeArray) {
if (node == null){
return count;
}
if( nodeArray != null ){
nodeArray[count] = node;
}
count++;
count = traverse(node.leftChild, count, nodeArray);
count = traverse(node.rightChild, count, nodeArray);
return count;
}
public static Node heapifyBinaryTree(Node root) {
//We don't know the size of array
int size = traverse(root, 0, null);
Node[] nodeArray = new Node[size];
// Fill nodes into array
traverse(root, 0, nodeArray);
// Sort array of nodes based on their values, using Comparator object
Arrays.sort(nodeArray, new Comparator<Node>() {
@Override
public int compare(Node m, Node n) {
int value1 = m.key, value2 = n.key;
return (value1 < value2 ? -1 : (value1 == value2 ? 0 : 1));
}
});
//Assign the left and right link to each node
for (int i = 0; i < size; i++) {
int left = 2 * i + 1;
int right = left + 1;
nodeArray[i].leftChild = left >= size ? null : nodeArray[left];
nodeArray[i].rightChild = right >= size ? null : nodeArray[right];
}
return nodeArray[0]; // Return new root node
}
}
Problem 3: Numbers are randomly generated and passed to a method. Write a program to find and maintain the median value as new values are generated.
First let’s understand about Median
Median is nothing but the middle most element in a set or ordered data. The condition here is that the data should be sorted either in ascending or descending.
For Example:
CASE-I: If number of elements(N) in data set is ODD then the Median = ((N+1)/2)th element in data set.
Data set = {2,5,8,9,10,12,18,20,24,28,26}
In above data set N = 11 which id ODD and (N+1)/2 = (11+1)/2 = 6, therefore Median= 6th element = 12
CASE-II: If number of elements(N) in data set is EVEN then the Median = AVERAGE of (N/2)th and ((N/2)+1))th element in data set.
Data set = {2,5,8,9,10,12,18,20,24,28,26,30}
In above data set N = 12 which id EVEN and N/2 = 12/2 = 6 and (N/2)+1) = 6+1=7 therefore Median= Average of 6th and 7th elements = (12 + 18)/2 = 15
The above problem can be easily solved using two priority heaps: a max heap for the values below the median, and a min heap for the values above the median.
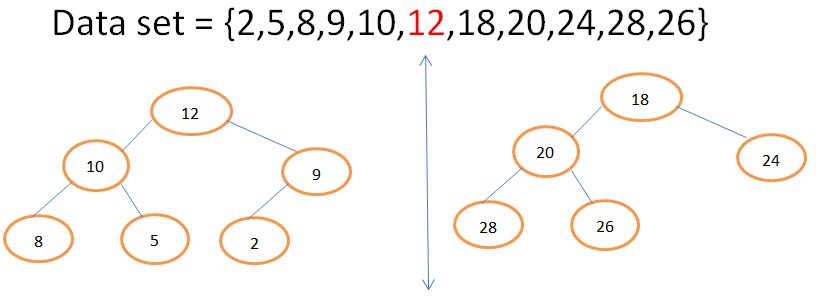
If both the heap size is equal then the Median will be the average of top element of MaxHeap and MinHeap, otherwise the Median will be the top element of larger heap.
When a new value arrives it is placed in the below heap if the value is less than or equal to the median, otherwise it is placed into the above heap. The heap sizes can be equal or the below heap has one extra. This constraint can easily be restored by shifting an element from one heap to the other. The median is available in constant time and updates are O(lg n).
Here I will use Java PriorityQueue collection since it doesn’t have size constraint.
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Random;
public class MedianFinder {
// By default priority queue is MinHeap in java
private PriorityQueue<Integer> maxHeap, minHeap;
private static final int INITIAL_CAPACITY = 10;
public MedianFinder() {
//Nothing to do for minHeap
minHeap = new PriorityQueue<Integer>(INITIAL_CAPACITY);
//To act like a max heap, reverse the default behavior with comparator
maxHeap = new PriorityQueue<>(INITIAL_CAPACITY, new Comparator<Integer>() {
@Override
public int compare(Integer i1, Integer i2) {
return (i1 > i2 ? -1 : (i1 == i2 ? 0 : 1));
}
});
}
public void addNewNumber(int randomNumber) {
if (maxHeap.size() == minHeap.size()) {
if ((minHeap.peek() != null) && randomNumber > minHeap.peek()) {
maxHeap.offer(minHeap.poll());
minHeap.offer(randomNumber);
} else {
maxHeap.offer(randomNumber);
}
} else {
if (randomNumber < maxHeap.peek()) {
minHeap.offer(maxHeap.poll());
maxHeap.offer(randomNumber);
} else {
minHeap.offer(randomNumber);
}
}
}
public double getMedian() {
if (maxHeap.isEmpty())
return minHeap.peek();
else if (minHeap.isEmpty())
return maxHeap.peek();
if (maxHeap.size() == minHeap.size()) {
return (minHeap.peek() + maxHeap.peek()) / 2.0;
} else if (maxHeap.size() > minHeap.size()) {
return maxHeap.peek();
} else {
return minHeap.peek();
}
}
//Generate some random numbers between 0 to 100
private int[] generateRandomArray(int size) {
int[] array = new int[size];
Random random = new Random();
for (int i = 0; i < size; i++) {
array[i] = random.nextInt(100); // between 0 to 100
}
return array;
}
public static void main(String[] args) {
MedianFinder medianFinder = new MedianFinder();
//If the number(N) of elements is Odd then median = (N+1)/2 th element
System.out.println("------N is ODD------");
int[] A1 = medianFinder.generateRandomArray(15);
System.out.println("Array: " + Arrays.toString(A1));
for (int a : A1) {
medianFinder.addNewNumber(a);
}
System.out.println("Median is: "+medianFinder.getMedian());
//Try to find median in sorted array
Arrays.sort(A1);
System.out.println("Sorted Array: "+Arrays.toString(A1));
// If the number(N) of elements is Even then median = AVG(N/2th, N/2th) element
System.out.println("------N is EVEN------");
medianFinder = new MedianFinder();
int[] A2 = medianFinder.generateRandomArray(16);
System.out.println("Array: " + Arrays.toString(A2));
for (int a : A2) {
medianFinder.addNewNumber(a);
}
System.out.println("Median is: " + medianFinder.getMedian());
// Try to find median in sorted array
Arrays.sort(A2);
System.out.println("Sorted Array: " + Arrays.toString(A2));
}
}
Output
--------
------N is ODD------
Array: [47, 35, 88, 25, 12, 75, 8, 53, 74, 18, 15, 51, 92, 4, 45]
Median is: 45.0
Sorted Array: [4, 8, 12, 15, 18, 25, 35, 45, 47, 51, 53, 74, 75, 88, 92]
------N is EVEN------
Array: [35, 59, 54, 41, 85, 71, 99, 30, 2, 67, 27, 18, 60, 87, 33, 2]
Median is: 47.5
Sorted Array: [2, 2, 18, 27, 30, 33, 35, 41, 54, 59, 60, 67, 71, 85, 87, 99]
Problem 4: Convert Max-Heap to Min-Heap or vice-versa.
This question I leave as an exercise for the reader. The logic is very simple- If you have to convert Max-Heap to Min-Heap – just call minHeapify(i) for i= (heapSize-1)/2 to 0. And for Min-Heap to Max-Heap call maxHeapify(i) in similar manner.
References:
- Cracking The Coding Interview- Gayle Laakmann McDowell
- Programming Interviews Exposed- John Mongan, Eric Giguère, Noah Kindler.
- Coding Interviews- Harry He

Leave a Reply